設問は「監視員が正方形プール(10メートル四方)の角にいて、プールの縁は秒速2メートル、水中は同1メートルで移動する。スタートからプール内で最も移動に時間のかかる場所まで、何秒で着くか」というもの。
詳細な説明は後で書く。
まず、監視員の位置を原点Oとする。残りの角を、Oから反時計回りにA, B, Cとする。そして、点Aがx軸上に、点Cがy軸上にあるように座標軸を設定する。
プールは直線y=xに関して対称なので、「最も移動に時間のかかる場所」は対角線OB上にあることは自明。(追記)そんなことはないですね。訂正。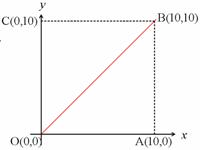
ということで早速OB上の点を探し始める……とややこしくなる。なぜややこしいかというと、監視員がプールの縁を歩くから。角を曲がってさらに歩いたりするケースも考えないといけない。ややこしい。
すこしでも簡単に考えたいので、とっかかりとして角を曲がらない泳ぎ方だけ考えたい。OからAまで歩くと5秒かかる。じゃあ、5秒まででプールのどの地点まで泳げるだろうか?
以下、プールの対象性を考慮して、三角形OABに着目して考えることにしよう。
5秒でどこまで泳げるか、を考えるには少し発想の転換が必要である。たとえば歩いたり泳いだりして5秒でX地点までたどり着いたとしよう。でももし、もっと速くX地点にたどり着くルートがあるとすれば、そのX地点は5秒で泳げる限界ラインよりも手前だということになる。逆に考えると、X地点まで最も速くたどり着けるルートを探してやる必要がある。
ということで、プールの任意の点までもっとも速くたどり着くルートを探そう。ルートというのは、要するにどこからプールに飛び込むかの問題だ。なぜなら、飛び込み地点が決まれば、あとは一直線に泳ぐのが一番速いからだ。もっと言うと、プールに飛び込む角度をどうすると一番速いかという問題になる。
三角形OAB内に点Pをとり、Pからx軸におろした垂線がx軸と交わる点をHとする。監視員がプールに飛び込む点をQとする。このときPまで最も速くたどり着くのはQがどこにあるときか。
飛び込む角度だけが問題になるので、計算を単純にするためOP=1としてしまおう。角POHはφとしておく。で、問題の角PQHをθとする。
点Oから点Qまで歩き、点Qから点Pまで泳いだときにかかる時間Tはφとθの関数となる。φを固定すると、θの値がどのようになったとき、時間Tが最小になるだろうか?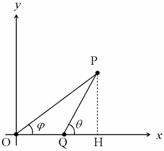
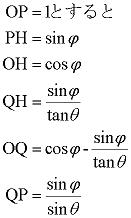

ということで、π/4 (=45°)π/3 (=60°)の角度で泳ぐのが最速とわかる。
(以下、あとで修正する)
こんにちは
返信削除面白い問題でしたので3日ぐらい考えています。
まだ解けていませんが、最速はπ/6の角度ではないでしょうか。
何度もすみません。
返信削除60度、π/3の間違いです。
う、確かにπ/3ですね。cosθ=1/2ですもんね。
返信削除不注意すぎる……
猪股さんの最速の角度の求め方はとてもエレガントで勉強になりました。
返信削除わたしはとてもドンくさい方法しか思いつきませんでした。
この問題、未だに解けないです。
何度もお邪魔してすみません。
返信削除ようやく解けました。
13.4946521345415565735655427635103秒
でよろしいでしょうか。
「監視員が正方形プール(10メートル四方)の角にいて、
返信削除プールの縁は秒速2メートル、水中は同1メートルで移動する。
スタートからプール内で最も移動に時間のかかる場所まで、何秒で着くか」
中学生のレベル三角比とピタゴラスの定理で答えられる問題みたい
です。
水中の速度と陸の速度が違うので、すべて水中の道のりに変換する
方法を考える。
まず、出発点Aからプールの縁のX点で水中に入りP点まで
行った道のりをA竏窒w竏窒oとすると、
(図アはA竏窒a竏窒b竏窒cの正方形で左下がA、右下Bにする。
点Pは点B寄りの点にする。)
図アのようにA竏窒wは陸の部分なので、水中の2倍進むから
A竏窒wの半分が水中の道のりになる。それをA1竏窒wで表すと
点Pに到達する最短距離の道のりは図イのように変換できる。
(図イはプールの右横にもう1つのプールを描く。
Bの10m右にC’、C’の10m上にD’
そして点Aからプールの外側下に角度30度で長い補助線AA’
を引きAA’C’が30度+90度+60度の直角三角形を描く。
この三角形の辺の比1:2:√3を使って、プールの縁の道のりを
水中の道のりに変換する。)
したがって、図ウの斜線の部分の中は変換後の水中での道のりは
10m以内であることがわかる。
そして10m以上の道のりは図エの三角形の部分に絞られる。
(図ウは右横のプールの点C’から補助線AA’に平行に
補助線C’Eを引くEはACとの交点 後は考えてください。)
図エの三角形の斜辺上の点Qが残りの辺からいちばん遠い所に
ある時、つまり、点Qから残りの2辺に垂線を下ろした時に
同じ距離になる点がいちばん時間のかかる点であることが
わかる。
その垂線の長さをhとすると10+hが求める時間になる。
三角形の比より
h:5(√3-1)-h=√3-1:√3+1
h=(10√3-15)/3
よって答えは10+h=5+10√3/3(秒)
なるほどー、とは言えこれはトリッキーですねえ。
返信削除凡人の私から見ると、"60度"に当たりがついていないとこの図は書けないと思いました。
図については後で別エントリに起こしてみます。
素晴らしい!
返信削除アイディアと論証の展開、文章構成、
全てにおいて驚愕しました。
これほどの素養があるなら専門書を読んでも
苦もなく理解できると思う。
学校の授業の進捗など無視してガロアみたいに
どんどん先に進むことをお勧めします。
ぜひ、フィールズ賞めざしてください。
いや縲怐A感動しました。
猪股さんのブログで好き勝手ほざいて
申しわけありませんでした。
物理的な考察をすると,これは屈折率2の物体から光を出した時の臨界角と考えることが出来ます。
返信削除なぜなら光はフェルマーの原理にしたがい最短の光学的距離(つまり最短時間)の経路をとおるからです。
屈折率が2ということは臨界角は sin(θ)=1/2
よって θ=π/6 となります。
すみません,屈折角の場合とθの置き方が異なるのでπ/2-π/6でπ/6ですね。
返信削除この手の問題を光の屈折で解くのは結構卑怯かもw
物理的な考察をすると,これは屈折率2の物体から光を出した時の臨界角と考えることが出来ます。
返信削除なぜなら光はフェルマーの原理にしたがい最短の光学的距離(つまり最短時間)の経路をとおるからです。
屈折率が2ということは臨界角は sin(θ)=1/2
よって θ=π/6 となります。
すみません,屈折角の場合とθの置き方が異なるのでπ/2-π/6でπ/6ですね。
返信削除この手の問題を光の屈折で解くのは結構卑怯かもw
大数に答え書いてあるね(笑)
返信削除大数に答え書いてあるね(笑)
返信削除愛知県にお住まいの山崎さん、はじめまして。
返信削除大学への数学で取り上げましたか。興味深い問題でしたからね。